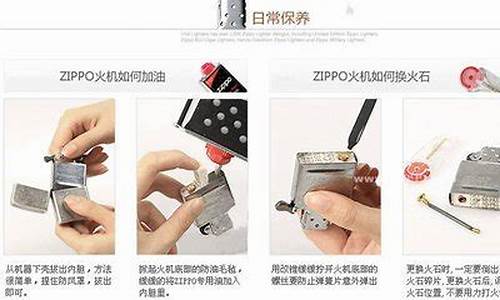
bx7 92汽油_bh23汽油

1.帮我出140道数学题，有答案，六年级上册的

2.带三点水的字有哪些

社区救援队个人装备配置清单

装备类别 名称 数量 备注

服装 救援服 1套 姓名牌、logo、反光条

雨衣 1件

大衣 1件

背囊 1个 防雨罩

腰带 1条

马甲背心 1件 多功能

腰包 1个

安全防护 救援靴 1双

防护手套 1双

护膝、护肘 1套

安全帽 1个 头灯、护目镜、

棉口罩 1个

防尘口罩 1个

多功能折叠刀 1把

偏光太阳镜 1副

餐具 1套

洗漱包 1套

水袋 1个

压缩干粮 3包 单兵自热食品

睡袋 1个 羽绒

睡袋 1个 抓绒

防潮垫 1个

军用指北针 1个

笔记本 1本

记号笔 2个

口哨 1个

对讲机 1个

D型锁 2个

O型锁 2个

8字环 1个

救援绳 1条 长10米，直径8毫米左右

斧头 1把

双向滑轮 1个

胸部上升器 1个

照明设备

警示灯 5个

银光棒 5个

强光手电筒 1个

社区救援队公共装备配置清单

设备分类 器材名称 规格

气体检测设备 可燃气体探测仪 EX2000 型

氧气探测仪 OX2000 型

可燃气体探测仪 Pac Ex 2 型

漏电检测设备 漏电检测仪 Will—Burt TAC Hot Stick 型

仪器搜索设备 光学生命探测仪 LD6C 型

热成像生命探测仪 TIV—FARBE 型

液压破拆设备 重型液压扩张钳 SP3260+ 型

轻型液压扩张钳 SP3230+ 型

重型液压剪切钳 CU3040+ 型

轻型液压剪切钳 CU3031+ 型

小型液压剪切钳 HMC8U 型

重型液压扩张剪切钳 CT3150+ 型

开缝器 PW3624+ 型

内燃破拆设备 破碎机 BH23 型

链锯 STIHL MS460 型

无齿锯 TS 400 型

电动破拆设备 常规凿岩机 TE705 型

“”快速钢筋切断器

双轮异向据 Wimutec 2747R 型

充电式往复据 CR 24DV 型

切割链锯 ICS 613GC 型

切割链锯 ICS 633GC 型

电动液压泵 HE42 型

水泥切割机 PARTNER K3600 型

液压钻孔机 IFTON M5 型

手动破拆设备 组合撬棍 MT6 型

组合工具 SOS (KAMV) 型

液压顶撑设备 液压顶杆 RA3322+ 型

液压顶杆 RA3332+ 型

双级液压顶杆 TR3340+ 型

边缘抬升器 TJ3610 型

手动液压千斤顶 HLJ50A6 型

气动顶升设备 高压起重气垫 SP1~SP68 型

救援设备 汽油发电机 EF6600 型

防水发电机 BSKA6.5 型

大型液压泵 DPU60P 型

小型液压泵 TPU15+ 型

手动液压泵 HTW1800BU 型

内燃充气机 JIIB 型

碳纤维高压气瓶 BEMAEX 6.8L 型

救援设备 正压排烟机 TYPHOON 型

封管器 HPS60AU 型

牵拉器 S35 型

小型牵拉器 HIT 6/10/16/32 型

救援三脚架

攀援救生套件 OZKAR 型

空气呼吸器 GPAL

救援静力绳 纤维（直径10.5mm）

篮式担架

铲式担架

折叠担架

脊柱板担架

卷式担架

照明设备 气动升降照明灯 QT6M 型

强光手电筒

线盘

救援工具 大锤

小锤

钢锯

手锯

撬棍

斧子 平头

斧子 尖头

通讯设备 对讲机

3G

宿营设备 指挥帐篷

双人冬季帐篷

双人夏季帐篷

生活设备 便携式野战炉灶

炊具

帮我出140道数学题，有答案，六年级上册的

从这些习题中去理解概念吧

六年级数学总复习练习

总复习1——数的认识

一、填空。

1．在18、0.3、9.16、0、1、0.2604、0.806中整数有（ ），自然数有（ ），小数有（ ），有限小数有（ ），循环小数（ ），纯循环小数有（ ），混循环小数有（ ）。

2．从个位到千亿位，分成（ ）级，它们是（ ）；分别包括（ ）数位。

3．小数点左边部分叫（ ）部分，右边部分叫做（ ）部分；小数点左边第二位是（ ），计数单位是（ ）。

4．4536100是（　）位数，最高位是（　）位，最高位上的数是（　　），表示（　　）。

5．一个八位数，它的最高位上的数字是8，十万位上的数字是4，其他各位上的数字都是0，这个数写作（ ）。

6．在79648000中，7在（ ）位上，计数单位是（ ）；6在（ ）位上，计数单位是（ ）；8在（ ）位上，计数单位是（　）。

7、、⑴6005000读作: (2)0.015读作:

(3)80040903读作: (4)105.206读作:

(5)1060050860读作: (6)20815 读作:

8.⑴三十五万八千 写作: ⑵零点 写作:

⑶四千零六万零七百 写作： ⑷九又十七分五 写作:

9. 35个0.1和63个0.01组成的数是

10、⑴0.28有 个百分之一; 1.3里有13个 ; 个千分之一是3.75

10 有三个”6”和两个”0”能组成的最大五位数是 ,最小五位数是 ,能组成两个”0”都读出来的五位数是 .

二 判断.

1.在一个八位数中,每相邻的两个计数单位之间的进率是10. ( )

2.一个七位数,它的最高位是百万位. ( )

3. 4.3和4.30的计数单位相同. ( )

4. 在读数或写数时,都要从高位开始. ( )

5. 小数都比整数小. ( )

6. 百分数都比1小. ( )

7. 比0.57大比0.59小的数只有一个. ( )

8. 一个数的中间连续有两个0,一定要读一个零.( ).

9. 万级的最低位是万位.( )

10. 一根4米长的钢筋,锯成8段,每段长12 米.

总复习2——分数和小数

一 判断

1. 1个百分之一等于10个千分之一. ( )

2. 四位小数一定小于五位小数. ( )

3. 最小的三位小数是 0.001. ( )

4. 如果分数单位不变,大于19 又小于59 的真分数只有3个.

5. 两个自然数相除,商一定比其中较小的自然数大.

6. 一个整数省略万后面的尾数后约等于20万,这个数最大的数是199999.( )

7.整数不一定都大于小数. ( )

8. 如果ab 是分数,那么ab 的分子必定大于分母.( )

二 把下面各数改写成用"万"作单位的数.

⑴ 95630000

⑵ 86700000

⑶ 6857000

⑷ 82345600

三 把下面各数写成用"亿"作单位的数.

保留一位小数: ⑴273400000 ⑵4000000

保留两位小数: ⑴248300000 ⑵9637800000

保留三位小数: ⑴843250000 ⑵735115000

四 把下面各小数四舍五入.

1. 精确到十分位: (1)4.36 (2)0.954 (3)2.476

2. 精确到百分位: (1)0.758 (2)1.482 (3)6.999

3. 精确到千分位: (1)3.1456 (2)0.6783 (3)9.3584

五 把下面各分数化成百分数.

1120 134 1230 189

六 化下列各百分数为小数或整数.

42% 80.6% 200%

七 把下列各百分数化成分数.

0.9% 12% 22.4%

八 比较大小.

1.把下面每组中三个分数,用小于号连接起来.

⑴36 56 38 (2)716 916 718

2.先通分,再比较大小,并用大于号连接起来.

23 34 57 47 914 1528

3. 比较下面各数并用小于号连接起来

0.955 2425 9.5% 0.

0.95 0.95

总复习3——约数、公因数和公倍数

一 选择.(将正确答案填在括号里)

1. 8.6能( ) ①整除2 ②被2整除 ③被2除尽

2.数a能被3整除,( )被9整除,数a能被9整除,( )被3整除.

①一定能 ②不一定能 ③不可能

3 只有质因数2的数是( )

①6 ②8 ③12

4 因为63=7×9,所以7和9都是63的( )

①约数 ②公约数 ③公倍数

5.一个质数有( )个约数.

①1 ②2 ③无数

6.成为互质数的两个数,( )

①只有公约数1 ②都是质数 ③一个质数,一个合数

7.两个质数的积一定是( )

①合数 ②奇数 ③偶数

8. 两个数的积一定是它们的( ).

①公约数 ②公倍数 ③最小公倍数

9.把0.068的小数点去掉后是原数的( )

①2倍 ②100倍 ③1000倍

10. 35 的分母增加3倍,要使分数的大小不变,分子应该( ).

①扩大2倍 ②扩大3倍 ③扩大4倍.

二 填空

1. 最小的自然数是( );既不是质数又不是合数的整数是( ).

2. 30以内最小的合数是( );最大的质数是( );它们的和是( ),这个和等于质数( )加上质数( ).

3. 在 1、2、27、33、47、53、68、84这些数中。

①既是奇数又是合数

②既是偶数又质数的有③既是合数又是偶数的有（　）

4．60的所有约数是（　）其中是质数的有（　）。

5．用一个数去除12、16、28，正好都能整除，这个数最大是（ ）。

6．能被7、9、12整除的最小自然数是（ ）。

7．两个数的积是96，它们的最大公约数是4，这两个数分别是（ ）和（ ）。

8．甲乙两数的最大公约数是3，最小公倍数是45，如果甲数是9，那么乙数是（ ）；如果甲数是45，那么乙数是（ ）。

9．把1236 的分母缩小12倍，要使分数的大小不变，分子应该（ ）；分数变成（ ）。

10．当分数29 的分子加上4时，为了使分数的大小部标，分母要加上（ ）。

总复习4——分数的计算

一、写出下面算式的意义。

1．84×310

2．84÷0.3

二、错题订正。（说明错误原因，算出正确得数）

1．45.2+2.74=72.6

2. 22.1-1.56=6.5

3. 34 +45 =720

4. 2-37 =137

5. 3118.6÷6.2=53

6. 70.3÷10%=7.03

三、在○里填入">""<"或"="。

1． 135 ×89 ○89

2. 132×34 ○132×3÷4

3. 37 ÷32 ○37

4. 15÷35 ○15÷3×5

四、计算下面各题，并验算。

1．4815÷45

2. 0.35×2.4

3. 32 -78

4. 59 ÷2527

5. 12.05+3.5

6. 75 ×314

总复习5——分数的计算

一、用简便方法计算下列各题。

1．437+998

2．372-199

3．0.125×3.7×8

4. 2.5×13×40

5. 0.25×(0.4+4)

6. 5-59 -49

7. 87 ×36×78

8. 28×23 +2×23

9. (15+52 )×52

10. 57 +56 +27 +16

11. 25 ×99+25

12. (35 -12 )×53

13. 25 ÷3+35 ×13

14. 13 ÷49 +13 +14

15. 3-35 ×521 -67

16. 29 +12 ÷45 +38

二、计算下面各题。

1．25 +27 ÷37

2． 8×3.4+3.6÷0.6

3. 2-815 ×916

4. 0.3×7.5-0.375×2

5. 25 ×43 +15 ÷34

6. 34 ÷(1-12 -14 )

7. (12 -38 )÷34

8. 10÷59 +19 ×6

9. 79 ÷135 +29 ×513

10. (12 +17 -712 )÷17

11. 3÷0.01+40×0.5

12. (14 +45 )÷73 +710

总复习6—分数的计算

1．78 ×34 ＋14 ×78

2．23 ＋13 ÷23

3. 20-18 ×45

4. 2.2×3.7+6.3×2.2

5. (45 -23 )×154

6. 114 ×(14 +112 )

7. [1-(38 +14 )]÷14

8. 65 ×(23 +32 )÷85

9. 67 ÷[(47 -12 )×25 ]

10. [1-(13 +115 )]÷45

二、文字题。（用综合算式解答）

1． 12 减去18 的差乘35 ，积是多少？

2．1减去4的16 ，所得的差再除35 ，商是多少？

3．0.8乘1.25的积，加上21除以4.2的商，得多少？

4． 45 乘4的倒数，所得的积比12 少多少？

5．25 加上8个15 的和，被13 除，商是多少？

6．910 减去13 除320 的商，所得的差与59 相乘，结果是多少？

代数初步知识

总复习7——方程

一、判断

1．a除以b商减去c可以写成ab -c ( )

2. 0.32=0.9 ( )

3. 使方程左右两边相等的未知数的值，叫做方程的解。

4．因为方程是一个等式，所以等式也就是方程。

5． 长方形的长是a厘米，宽是5厘米，它的周长是（2a+10）厘米，面积是5a平方厘米。

二、选择（将正确答案的序号填在括号里）

1．a3表示（　）

①a+a+a ②a×3 ③a.a.a

2.下面的式子中，是方程式的是（　）。

①3x+15 ②5-x>3 ③5x=18-4

3. 2+2a1+a 这一分数，a不论是任何自然数，这个式子的值是（　）。

①2②1 ③0

4．a与b的和的18 用式子表示是（　）。

①a+18 ②18 ＝a＋b ③18 a+b

5. 自然数a和b，当a+3=b-3时，则（　　）。

①a>b ②a<b ③a=b

6. 一个两位数，它们十位上的数字是6，个位上的数字是a,表示这个两位数的式子是（　）。

①6+a ②6a ③6×10+a

7. 四个数的平均数是15,如果每个数增加a,那么这四个数的和是（　）。

①15×4+a ②15+4a ③(15+a)×4

8. 三角形的面积是s平方米，其中高是4米，那么底是（　）。

①2s÷4 ②s÷2÷4 ③s÷4

9. 某水果店运进苹果m千克，比梨的4倍多n千克，求运进梨的千克数的算式是（　）

①m÷4-n ②(m-n)÷4③(m+n)÷4

10. 甲袋有a千克大米，乙袋有b千克大米，如果从甲袋拿出8千克放入乙袋，那么甲乙两袋重量相等。列成等式（ ）。

①a+8=b-8 ②a-b=8×2 ③(a+b)÷2=8

三、解简易方程

1． X+0.2=1.4

2. 320-x=7.2

3. 17 x=314

4. 45 ÷x=89

5. 0.8x-14.7=1.3

6. (10-7.5)x=0.125×8

7. x×(1-37.5%)=58

8. 13 x+14 x=23

9. 38 x-25%x=4

10. x-0.75x-0.25=1

四、列出方程，求出方程的解。

1． X与5的和的3倍等于180，求x.

2. 一个数的4倍，加上12 的和是1，求这个数。

3． 一个数减去它的20%后是16，求这个数。

4． X的23 比x的25%多20，求x.

5．一个数的75%等于120的34 ，求这个数。

6．30比一个数的75%少6，求这个数。

总复习8—比例

一填空：

1、 两个数相除又叫做（ ）。

2、除法里的（　），分数里的（　　），比的( )不能为零

3. 比是表示数量间的关系,除法是一种( );分数是( ).

4. 比例10:12=15:18写成分数形式是( ),写成乘法算式是( ).

5. 用20以内的四个合数组成二个比的两个比值都等于112 的比例式如( ).

二 把下面的比化简后求比值.

1. 3:0.12

2. 310 :75

3. 0.6:40%

4. 1厘米:1千米

5. 1.2吨:2.5吨

三 问答

1. 4:12和0.35:1.05能不能组成比例?为什么?

2. 下面哪一组数中的两个比可以组成比例?把能组成比例的写出来.

(1) 3:15和8:40

(2) 0.3:1.2和0.5:2

(3) 2120 78 14

(4) 58 25

四 解比例

1. 89 与x的比等于23 和3的比,x等于多少?

2. 9:3=36:12,如果第三项减去12,那么第一项应减去多少?

3. 4:7=12:21,如果第二项扩大3倍,那么第三项应该是多少?

4. 12 :23 =34 :1 如果第四项改为5,那么第二项应改为多少?

五 应用题

1. 一张零件图的比例尺是8:1,如果在图上量得某线段长56毫米,其实际长度是多少?

2. 长6米,宽4米的长方形花坛,在比例尺为1:200的图纸上,长应画多少厘米?宽应画多少厘米?

3. 一块长方形水田,在比例尺为1:2000的地图上,它长2.5厘米,宽1.5厘米;水田的实际面积是多少平方米?

4. 在比例尺是1:4的图纸上,量得一个零件的长度是5毫米,这个零件的实际长度是多少厘米?如果把这个零件用8厘米的长度画在另一张图纸上,这张图纸的比例尺硬实多少?

5. 实际距离500千米在三张比例尺为15000000 ,1:400000, 图纸上各应画多少厘米?

6. 一块直角三角形钢板用1200 的比例尺画在图上,这个图的两条直角边共长5.4厘米,它们的比是5:4,这块钢板的实际面积是多少?

总复习9—比例

一 填空

1. 1:0.25的比值是( );如果后项乘以4,要使比值不变,前项应该变成( );如果前、后项都除以0.25，比值是（ ）。

2．一个比例中，两个内项的积是13.5，一个外项是9，另一个外项是（ ）。

3. 在一个比例中,两个外项互为倒数,其中一个内项是152 ,另一个内项是( ).

4. 如果A=BC ,那么当 一定时, 和 成反比例;当 一定时, 和 成正比例.

5. 甲数的45 等于乙数的34 ,甲数与乙数的比是( )

6. 减数相当于被减数的47 ,差与减数的比是( ).

二 解比例

1. 8:x=24:15

2. x:0.15=3.6:0.9

3. 1.2x =45

4. 110 :x=15 :14

5. 2.4:1.6=12:x

6. 4:23 =x:16

三 判断下列两种量是不是成比例,成什么比例.

1. 单位面积产量一定,种植面积与总产量.

2.织布总量一定,每小时织布数与时间.

3.三角形面积一定,它的底与高.

4. 被减数一定，减数与差.

5. 平行四边形的底不变,高与面积.

6. 做一项工程,工作效率与完工时间.

7. 任务一定,已完成数量与未完成数量.

8.圆柱体积一定,底面积与高.

9.总土量一定,每天挑土量与挑的天数.

10.两个齿轮咬合转动时,转速与齿数.

11.汽车从甲地开到乙地,行车时间与速度.

12.比的前项一定,比的后项与比值.

总复习10——分数解决问题

一、解答下面各应用题

1. 修一条公路,甲队每天修全长的115 ,乙队每天修全长的112 ,乙队每天比甲队多修几分之几?

2. 一个长方形花圃,宽78 米,比长少15 米,长有多少米?

3. 一列火车每小时行75千米,34 小时行多少千米?

4. 六(2)班同学分三组种树,第一组种120棵,第二组种的是第一组的54 ,第一组种的是第三组的56 ;第二组、第三组各种多少棵？

5．某乡去年造林12460平方米，是原的76 倍，求原造林多少平方米？

6．建筑工地运来8000块青砖，运来的红砖是青砖的85%，运来红砖多少块？

7．一桶油，到出80%，刚好倒出36千克，这个油桶能容油多少千克？

8．把稻子磨成大米可以出糠皮27%，磨6000千克稻子能出多少糠皮？出多少大米？

二、给下面各题补上一个条件或问题成简单应用题再解答。

1．有花布24.5米， 可做多少件衣服？

2．商店运进两批苹果，第一批800千克， ，第二批苹果重多少千克？（编一道用乘法算的分数应用题）

3．某工厂现在制造一台机床要用20小时，是原来的56 ， ？

总复习11—解决问题

一、只列综合算式、不计算。

1．3支钢笔的价钱与4支圆珠笔的价钱相等，圆珠笔的单价是1.80元，钢笔的单价是多少元？

2．新华书店第一天卖出新书680本，比第二天少卖出50本，第三天卖出的是第二天的1.5倍。第三天卖出新书多少本？

3．同学们参加植树活动，五(1)班种树143棵，比五(2)班多种15棵，两个班一共种树多少棵？

4．要修一段12.5千米长的公路，已经修了7.8千米，已修的比未修的多多少千米？

5．粮店里面粉每千克3.8元，大米每千克3元。程叔叔买回面粉和大米各10千克。他付出100元，应找回多少元？

二、列式解答

1．百货公司第一天卖出书包56个，第二天卖出同样的书包120个，第二天比第一天多收入2240元,第二天收入多少元?

2. 风实农具厂制造镰刀6480把,原18天完成,实际每天多制造72把,实际几天就完成任务?

3. 红叶服装厂做660套衣服,已经做了5天,平均每天做75套.剩下的要3天做完,平均每天要做多少套?

4. 某机械厂原五月份生产零件18600个,结果提前4天不仅完成了任务,还比原多生产30个,实际每天生产零件多少个?

5. 水果店运来6筐苹果和6筐梨共重390千克,已知每筐苹果比每筐梨重5千克.求每筐苹果每筐梨各重多少千克?

6. 甲瓶里有酒精470毫升,乙瓶里有酒精190毫升,为了使甲瓶酒精是乙瓶酒精的2倍,应该把甲瓶的酒精倒入乙瓶多少毫升?

总复习12——分数问题

一 选择题.

1. 一个工厂制造一台机器原来要用129小时,改进技术以后只用86小时;原来制造126台机器的时间,现在可以制造多少台?

①86×126÷129 ②129×126÷86 ③129×86÷126

2. 养牛场5天割草3000千克,实际每天比多割150千克,割这些草实际用多少天?

①3000÷150×5 ②3000÷5÷150 ③3000÷(3000÷5+150)

3. 一段公路,由甲、乙两队合修6天可以完成，由甲队单独修要10天完成。由乙队单独修要几天？

①1÷（16 +110 ） ②1÷（16 -110 ） ③16 ×110

4．修一条水渠，甲队单独修要15天，乙队单独修要12天，两队合作几天可完成水渠的910 ？

①910 ÷（115 +112 ） ②1÷（115 +112 ） ③（1-910 ）÷（115 +112 ）

二、列式解答

1．一件工作由甲、乙两人合做要20天完成，由乙单独做要用30天；甲每天完成这件工作的几分之几？甲单独做完成这件工作要多少天？

2．从甲港到乙港，A船要8小时，B船要12小时。两船同时从两港相对开出；几小时后两船间的距离为两港距离的58 ？

3．建筑工地有水泥16.5吨，已经用了5天，平均每天用水泥1.8吨。剩下的水泥如果每天1.5吨，还可用多少天？

4．学校准备买26个篮球，每个价格为13.30元。后来从买篮球的钱里拿出一部分买了排球14个，每个价格为7.60元，这样还能买篮球多少个？

5．一份稿件，由一人单独抄，甲要12小时，乙要10小时，丙要15小时，如果由三人合抄，多少小时可抄完这份稿件的12 ？

6．一项工程由甲、乙两个工程队合做要20天，由甲工程队单独做要30天，现在先由两队合做4天，余下的工程由乙队单独做，还要多少天才能完成？

总复习13——解决问题

一、列方程解应用题

1．某建筑队修筑一段公路，原每天修56米，15天完成，实际上每天多修4米，实际用了几天？

2.师徒两人要加工360个零件,前4小时加工240个,照这样计算,剩下的零件还要几小时加工完?

3.水果店运来苹果20筐,梨10筐,共重1420千克;已知每筐苹果重26千克,每筐梨重多少千克?

4. 精工车间接受加工1440只精密零件的任务,原20天完成,实际头4天就加工出360只,照这样的工作效率可以提前几天完成任务?

5.粮店运来大米,面粉共3700千克,已知运来的面粉比大米的2倍多100千克,运来大米、面粉各多少千克？

6*一队少先队员乘船过河，如果每船坐15人，还剩9人，如果每船坐18人，则剩余1只船，求有多少只船？

总复习14——分数、解决问题

一、填空

1．火车的速度是汽车的45 ；标准量是（ ），比较量是（ ）。

2．一条公路已修了全长的47 ，把（ ）看作单位“1”，（ ）是单位“1”的47 ，还剩下全长的（ ）未修。

3．山前机械厂九月份产值比八月份增加38 ，九月份产量是八月份的（ ）。

4．一种羊皮大衣因季节性调价，现价比原价降低25%，表示现在售价是（ ）的（ ）%

5．六年级一班男生人数是女生人数的35 ，男生人数占全班人数的（　）％

二、选择

1．唐山市现有建筑面积1800万平方米，比地震前多500万平方米，增加了（　）

①518 ②513 ③1318

2．甲数是乙数的65 ，那么乙数是甲数的（　），甲数比乙数多（　），乙数比甲数少（　）。

①20% ②56 ③16

三、应用题

1．一块长方形地，长160米，宽比长短14 ，这块地宽是多少米？面积是多少平方米？

2．有30袋大米共重2400千克，如果每袋大米多装25%，每个袋子能多装多少千克大米？3 工程队原一周修路36千米，实际修了45千米，实际修的占原的百分之几？实际比原多修百分之几？

4 工程队修一条路，第一天修了全长的14 ，第二天修了全长的37.5%，已知第二天比第一天多修200米。这条路全长是多少米？

5．某工厂有职工500人，某天出勤率是98%，其中女职工出勤人数占出勤职工总人数的60%，这天出勤的女职工有多少人？

6．某工厂男职工比全厂职工总人数的60%少24人，女职工有124人，全厂有职工有多少人？

总复习15——解决问题

一、选择。

1．组成一个比例要有（ ）比，并且这几个比要（ ）

①相等 ②相同 ③二个

2．甲数是乙数的k倍；甲数与乙数成（ ）

①正比例 ②反比例 ③不成比例

3．在一定时间里，做一个零件所用的时间和做零件的个数（ ）

①不成比例②成正比例③成反比例

4．一件工程单独做，乙要8天，甲要6天；甲乙两人工作时间比是（ ）工作效率比是（ ）

①4：3②3：4③113 ④34

二、用比例方法解

1．五（1）班师生进行野营拉练，3小时走了12千米，按这个速度前进，再走30千米还需几小时？

2．某部队行军，每小时走6千米，需10小时到达目的地。按照命令必须在8小时内赶到，每小时至少要走多少千米？

3．红星机械厂加工一批螺丝帽，若每天生产1500个，要12天才能完成，如果每天生产2000个，多少天就能完成？

4. 小明的手表在8小时里快了2秒钟,如果不加调整一个星期后会快多少秒?

5.王老师要翻译一本书,7天完成,平均每天翻译30页.如果每天翻译42页,要用多少天?

6.红山安装人工喷雨水管,头3天装了225米,按同样的速度,前后共用20天才把水管全部装好,这条水管共长多少米?

总复习16——解决问题

一 只列式不计算

1. 军民合修一条"军民渠",6天修678米,照这样的速度计算,修1695米的水渠,需要多少天?

2. 6台织布机9小时能织布756米,照这样计算,8台织布机12小时能织布多少米?

3. 300克蜂蜜里,含有103.5克葡萄糖;5千克蜂蜜里,含有多少克葡萄糖?

4. 甲、乙两车同时从同一地点向相反方向开出,甲车每小时行50千米,乙车每小时行40.5千米,3小时后两车相距多少千米?

5. 一条街长1672米,甲、乙两个学生从这条街的两端同时相向而行.甲骑自行车每分钟行350米;乙步行,经过4分钟后两人相遇,乙每分钟行多少米?

二、用两种方法解答下面各题.

1. 小云0.5小时摘苹果7千克,照这样计算,要摘45.6千克苹果需要几小时?

2. 一辆汽车行驶10千米节约汽油35 千克,照这样计算行驶150千米,可以节约汽油多少千克?

3. 用同样的方砖铺地,铺18平方米要用612块;如果铺30平方米,要用方砖多少块?

4. 果园里橘树的棵数是柑树的57 ,已知橘树比柑树少70棵,橘树和柑树各有多少棵?

5. 一段公路长60千米,甲队单独修10天完成,乙队单独修15天完成.两队合修几天完成?

6*小明看一本故事书,每天看15页,看了4天,后又看了全书的15 ,这时还剩下全书的15 没看,这本故事书共多少页?

7* 学校锅炉房原来存有大小两堆煤,共重24吨,在小堆煤上又加上4吨,从大堆煤里用去14 后,两堆煤的重量正好相等,求大小两堆煤原来各是多少吨?

总复习题17—单位

一、填空。

1．在括号里填上合适的计量单位。

（1）小英身高148（ ）。

（2）福州到厦门距离约是310（ ）。

（3）张文同学的体重35.6（　）。

(4)一个鸭蛋重32（　）。

(5)一本算术课本封面面积约为300( )

(6)一只瓶子的容积是500（　）。

(7)一节课上40（　）。

(8)东风牌卡车载重量是5（　）.

(9)一块特香包体积约是2( ).

(10)我国货币单位中最大的是( ),最小的是( ).

2.在下列括号里填上适当的数:

(1)4米=( )分米=( )厘米

(2)5.6千克=( )克

(3)1.2小时=( )分

(4)6300平方厘米=( )平方分米=( )平方米

(5)2.3平方千米=( )公顷=( )平方米

(6)438 吨=( )千克

(7)345 元=( )分

(8)93000立方厘米=( )毫升=( )升

二 选择.

1.一张试卷的面积约10( ).

①分米 ②米 ③平方厘米 ④平方分米

2. 今年第一季度是( )天.①②③④

①88 ②89 ③90 ④91

3.下面年份属于闰年的是( )年.

①1900 ②1986 ③2000 ④2100

4. 面积是1平方千米的正方形的边长是( ).

①10000米 ②100米

③100米 ④10米

5. 一个正方体的棱长总和是6分米,这个正方体的体积是( )立方分米.

①18 ②14 ③12 ④1

6. 一个杯子的容积是1.5升,这个杯子装满水后,杯子的( )是1.5( ).

①容积 ②体积 ③升④立方分米

总复习

一 判断题.

1. 公元年份能被4整除的,这一年不一定是闰年.

2.一年有四个季度,第四季度和第三季度的天数总是相等的.

3. 4升和4千克一样重.

4. 0.03千米等于30米.

5. 18小时15分=18.15小时.

6. 边长是4分米的正方形,周长和面积相等.

7. 1立方米钢铁重7.8吨,1立方分米的钢铁重7.8千克.

8. 小明出生于年2月29日,到2000年2月29日;他一共过5个生日.

二 在括号里填上适当的数.

1. 450米=( )千米

2. 6米3厘米=( )米

3. 7.8千克=( )克

4. 3.2小时=( )小时=( )分

5. 4吨60千克=( )千克=( )吨

6. 650毫升=( )升=( )立方厘米

7. 6.3平方米=( )平方分米=( )平方厘米

8. 8平方分米9平方厘米=( )平方厘米

9. 3.5公顷=( )平方米=( )平方千米

10. 0.07立方米=( )立方分米=( )立方厘米

11. 0.005立方米=( )升=( )毫升

12. 3725 元=(　)元（　）角（　）分

三　在下表的空格里填上适当的数．

小数 分数 单名数 复名数

2.08吨

513200 升

312分钟

6立方米8立方分米

四 解答题

1. 1888年这一年有多少天?有多少个星期?还余多少天?

2. 今天是星期二,从今天算起到第100天是星期几?

3.* 某年8月份中,雨天比晴天少13 ,阴天比晴天少35 ,这个月晴天、雨天、阴天各多少天？

4* 元旦是星期一，那么同年的国庆是星期几？第二年的元旦是星期几？

带三点水的字有哪些

6..甲、乙两车长度均为180米，若两列车相对行驶，从车头相遇到车尾离开共12秒；若同向行驶，从甲车头遇到乙车尾，到甲车尾超过乙车头需60秒，车的速度不变，求甲、乙两车的速度。

二车的速度和是：[180*2]/12=30米/秒

设甲速度是X，则乙的速度是30-X

180*2=60[X-（30-X）]

X=18

即甲车的速度是18米/秒，乙车的速度是：12米/秒

7.两根同样长的蜡烛,粗的可燃3小时,细的可燃8/3小时,停电时,同时点燃两根蜡烛,来电时同时吹灭,粗的是细的长度的2倍,求停电的时间.

设停电的时间是X

设总长是单位1，那么粗的一时间燃1/3，细的是3/8

1-X/3=2[1-3X/8]

X=2。4

即停电了2。4小时。

1.某小组做一批“中国结”，如果每人做5个，那么比多了9个；如果每人做4个，那么比少了15个，小组成员共有多少名？他们做多少个“中国结”？

设小组成员有x名

5x=4x＋15+9

5x-4x=15＋9

8.某中学组织初一学生进行春游，原租用45座客车若干辆，但有15人没有座位；若租用同样数量的60座客车，则多出一辆车，且其余客车恰好坐满。试问

（1） 初一年级人数是多少？原租用45座客车多少辆？

解：租用45座客车x辆，租用60座客车(x-1)辆,

45x+15=60(x-1)

解之得：x=5 45x+15=240(人）

答：初一年级学生人数是240人，

租用45座客车为5辆

9.将一批会计报表输入电脑，甲单独做需20h完成，乙单独做需12h完成．现在先由甲单独做4h，剩下的部分由甲，乙合作完成，甲，乙两人合作的时间是多少？

解;设为XH

1/5+1/20X+1/12X=1

8/60X=4/5

X=6

甲，乙两人合作的时间是6H.

10.甲乙丙三个数的和是53，以知甲数和乙数的比是4：3,丙数比乙数少2，乙数是（），丙数是（）

设甲数为4X.则乙为3X.丙为3X-2.

4X+3X+3X-2=53

10X=53+2

10X=55

X=5.5

3X=16.5

3X-2=16.5-2=14.5

乙为16.5,丙为14.5

11.粗蜡烛和细蜡烛的长短一样，粗蜡烛可燃5小时，细蜡烛可燃4小时，一次停电后同时点燃这两只蜡烛，来电后同时熄灭，结果发现粗蜡烛的长是细蜡烛长的4倍，求停电多长时间？

设停电x小时. 粗蜡烛每小时燃烧1/5,细蜡烛是1/4

1-1/5X=4(1-1/4)

1-1/5X=4-X

-1/5+X=4-1

4/5X=3

X=15/4

12.一个三位数,百位上的数字比十位上的数字大1,个位上的数字比十位上的数字的3倍少2,若将三个数字顺序颠倒后,所得的三位数与原三位数的和是1171,求这个三位数.

设十位数为x

则 100×（x+1)+10x+3x-2+100*(x+1)+10x+x+1=1171

化简得

424x=1272

所以:x=3

则这个三位数为437

13.一年级三个班为希望小学捐赠图书,一班娟了152册,二班捐书数是三个班级的平均数,三班捐书数是年级捐书总数的40%,三个班共捐了多少图书?

解：设⑵班捐x册

3x=152+x+3xX40%

3x=152+x+6/5x

3x-x-6/5x=152

4/5x=152

x=190…⑵班

190X3=570(本）

14.a b 两地相距31千米,甲从a地骑自行车去b地 一小时后乙骑摩托车也从a地去b地 已知甲每小时行12千米 乙每小时行28千米 问乙出发后多少小时追上甲

设乙出发x小时后追上甲，列方程

12（X+1）=28X X=0.75小时,即45分钟

15、一艘货船的载重量是400t,容积是860m^3.现在要装生铁和棉花两种货物,生铁每吨体积是0.3m^3,棉花每吨体积是4m^3.生铁和棉花各装多少吨,才能充分利用这艘船的载重量和容积?

设铁x吨，棉花为400－x吨

0.3x+4*(400-x)=860

x=200t

答案为铁和棉花各200吨

16、某电脑公司销售A、B两种品牌电脑，前年共卖出2200台，去年A种电脑卖出的数量比前年多6%，B种电脑卖出的数量比前年减少5%，两种电脑的总销量增加了110台。前年A、B两种电脑各卖了多少台？

设前年A电脑卖出了x台，B电脑卖出了2200－x台

去年A电脑为1.06x,B电脑为0.95（2200－x）

1.06x+0.95*(2200-x)=2200+110

x=2000

则A电脑2000台，B电脑200台

17.地球上面面积约等于陆地面积的29分之71倍，地球的表面积约等于5.1亿平方公里，求地球上陆地面积是多少？（精确到0.1亿平方公里）

设陆地的面积是X

X+71/29X=5.1

X=1.479

即陆地的面积是：1.5亿平方公里。

18. 内径为90毫米的圆柱形长玻璃杯（已装满水）向一个地面直径为131*131平方毫米，内高为81毫米的长方形铁盒到水，当铁盒装满水时，玻璃杯中水的高度下降多少？

设下降高度是X

下降的水的体积等于铁盒中的水的体积。

3.14*45*45*X=131*131*81

X=218.6

水面下降218.6毫米。

19.内径为120毫米的圆柱形玻璃杯，和内径为300毫米、内高为32毫米的圆柱形玻璃盘可以盛同样多的水，求玻璃杯的内高？

内径为120毫米的圆柱形玻璃杯,和内径为300毫米,内高为32毫米的圆柱形玻璃盘可以盛同样多的水

所以两个容器体积相等

内径为300毫米,内高为32毫米的圆柱形玻璃盘体积

V=π(300/2)^2*32=720000π

设玻璃杯的内高为X

那么

X*π(120/2)^2=720000π

X=200毫米

20.将内径为200毫米的圆柱形水桶中的满桶水倒入一个内部长、宽、高分别为300毫米、300毫米、80毫米的长方形铁盒，正好倒满。求圆柱形水桶的水高？（精确到毫米。派取3.14）

设水桶的高是X

3.14*100*100*X=300*300*80

X=229

即水桶的高是229毫米

21.某地下管道由甲工程队单独铺设需要12天，由乙工程队单独修设需要18天。如果有由两个工程队从两端同时想象施工，要多少天可以铺好？

解:设X天可以铺好

1/18X+1/12X=1

2/36X+3/36X=1

5/36X=1

X=1除以5/36

X=1乘以36/5

X=36/5

即要36/5天

7 某数的3倍减2等于某数与4的和，求某数．

解法1：(4+2)÷(3-1)=3．

答：某数为3．

解法2：设某数为x，则有3x-2=x+4．

解之，得x=3．

答：某数为3．

2、 方程（x+1）2－2（x－1）2=6x－5的一般形式是 。

3、 关于x的一元二次方程x2+mx+3=0的一个根是1，则m的值为 。

4、 已知二次三项式x2+2mx+4－m2是一个完全平方式，则m= 。

5、 已知 +（b－1）2=0，当k为 时，方程kx2+ax+b=0有两个不等的实数根。

6、 关于x的方程mx2－2x+1=0只有一个实数根，则m= 。

7、 请写出一个根为1，另一个根满足－1<x<1的一元二次方程是 。

8、 关于x的方程x2－（2m2+m－6）x－m=0两根互为相反数，则m= 。

9、 已知一元二次方程（a－1）x2+x+a2－1=0的两根为x1,x2，且x1+x2= ，则x1,x2= 。

10某木材场原有木材存量为a立方米，已知木材每年以20%的增长率生长，到每年冬天砍伐的木材量为x立方米，则经过一年后木材存量为 立方米，经过两年后，木材场木材存量为b立方米，试写出a,b,m之间的关系式： 。

二、选择题：（3’×8＝24’）

11、关于x的方程（m+1）x2+2mx－3=0是一元二次方程，则m的取值是（ ）

A、任意实数 B、m≠1 C、m≠－1 D、m>－1

12、下面是某同学在一次数学测验中解答的填空题，其中答对的是（ ）

A、 若x2=4，则x=2 B、若3x2=bx，则x=2

C、 x2+x-k=0的一个根是1，则k=2

D、若分式 的值为零，则x=2

13、方程（x+3）（x－3）=4的根的情况是（ ）

A、无实数根 B、有两个不相等的实数根 C、两根互为倒数 D、两根互为相反数

14、一元二次方程x2－3x－1=0与x2+4x+3=0的所有实数根的和等于（ ）。

A、－1 B、－4 C、4 D、3

15、已知方程（ ）2－5（ ）+6=0，设 =y则可变为（ ）。

A、y2+5y+6=0 B、y2－5y+6=0 C、y2+5y－6=0 D、y2－5y－6=0

16、某超市一月份的营业额为100万元，第一季度的营业额共800万元，如果平均每月增长率为x，则所列方程应为（ ）

A、100(1+x)2=800 B、100+100×2x=800 C、100+100×3x=800 D、100[1+(1+x)+(1+x)2]=800

17、已知一元二次方程2x2-3x+3=0，则（ ）

A、两根之和为－1.5 B、两根之差为－1.5 C、两根之积为－1.5 D、无实数根

18、已知a2+a2－1=0，b2+b2－1=0且a≠b，则ab+a+b=（ ）

A、2 B、－2 C、－1 D、0

三、解下列方程：（5’×5＝25’）

19、（x－2）2－3＝0 20、2x2－5x＋1＝0（配方法）

21、x(8＋x)＝16 22、

23、（2x－3）2－2（2x－3）－3＝0

四、解答题。

24、已知三角形的两边长分别是3和8，第三边的数值是一元二次方程x2－17x＋66＝0的根。求此三角形的周长。（6’）

25、某灯具店购了一批某种型号的节能灯，共用去400元，在搬运过程中不慎打碎了5盏，该店把余下的灯每盏加价4元全部售出，然后用所得的钱又购了一批这种节能灯，且进价与上次相同，但购买的数量比上次多了9盏，求每盏灯的进价。（6’）

26、在Rt△ABC中，∠C＝90°，斜边C＝5，两直角边的长a，b是关于x的一元二次方程x2－mx＋2m－2＝0的两根，（1）求m的值（2）求△ABC的面积（3）求较小锐角的正弦值。

α、β是方程 的两根，则α+β=__________，αβ=__________， __________， __________。

2．如果3是方程 的一个根，则另一根为__________，a=__________。

3．方程 两根为-3和4，则ab=__________。

4．以 和 为根的一元二次方程是__________。

5．若矩形的长和宽是方程 的两根，则矩形的周长为__________，面积为__________。

6．方程 的根的倒数和为7，则m=__________。

二、选择题

1．满足两实根和为4的方程是（ ）。

（A） （B）

（C） （D）

2．若k＞1，则关于x的方程 的根的情况是（ ）。

（A）有一正根和一负根 （B）有两个正根

（C）有两个负根 （D）没有实数根

3．已知两数和为-6，两数积为2，则这两数为（ ）。

（A） ， （B） ，

（C） ， （D） ，

4．若方程 两根之差的绝对值为8，则p的值为（ ）。

（A）2 （B）-2

（C）±2 （D）

三、解答题

1．已知 、 是方程 的两个实数根，且 ，求k的值。

2．不解方程，求作一个新的一元二次方程，使它的两根分别为方程 两根的平方。

3．如果关于x的方程 的两个实数根都小于1，求m的取值范围。

4．m为何值时，方程

（1）两根互为倒数；

（2）有两个正根；

（3）有一个正根一个负根。

解方程（1）(3x+1)2=7 （2）9x2-24x+16=11

用配方法解方程 3x2-4x-2=0

用公式法解方程 2x2-8x=-5

用因式分解法解下列方程：

(1) (x+3)(x-6)=-8 (2) 2x2+3x=0

(3) 6x2+5x-50=0 (选学） (4)x2-2( + )x+4=0 （选学）

用适当的方法解下列方程。(选学）

（1）4(x+2)2-9(x-3)2=0 （2）x2+(2-)x+ -3=0

（3） x2-2 x=- （4）4x2-4mx-10x+m2+5m+6=0

求方程3(x+1)2+5(x+1)(x-4)+2(x-4)2=0的二根。

用配方法解关于x的一元二次方程x2+px+q=0

一）用适当的方法解下列方程：

1. 6x2-x-2=0 2. (x+5)(x-5)=3

3. x2-x=0 4. x2-4x+4=0

5. 3x2+1=2x 6. (2x+3)2+5(2x+3)-6=0

（二）解下列关于x的方程

1.x2-ax+-b2=0 2. x2-( + )ax+ a2=0

选择题

1．方程x(x-5)=5(x-5)的根是（ ）

A、x=5 B、x=-5 C、x1=x2=5 D、x1=x2=-5

2．多项式a2+4a-10的值等于11，则a的值为（ ）。

A、3或7 B、-3或7 C、3或-7 D、-3或-7

3．若一元二次方程ax2+bx+c=0中的二次项系数，一次项系数和常数项之和等于零，那么方程必有一个

根是（ ）。

A、0 B、1 C、-1 D、±1

4． 一元二次方程ax2+bx+c=0有一个根是零的条件为（ ）。

A、b≠0且c=0 B、b=0且c≠0

C、b=0且c=0 D、c=0

5． 方程x2-3x=10的两个根是（ ）。

A、-2，5 B、2，-5 C、2，5 D、-2，-5

6． 方程x2-3x+3=0的解是（ ）。

A、 B、 C、 D、无实根

7． 方程2x2-0.15=0的解是（ ）。

A、x= B、x=-

C、x1=0.27, x2=-0.27 D、x1=, x2=-

8． 方程x2-x-4=0左边配成一个完全平方式后，所得的方程是（ ）。

A、(x-)2= B、(x- )2=-

C、(x- )2= D、以上答案都不对

9． 已知一元二次方程x2-2x-m=0，用配方法解该方程配方后的方程是（ ）。

A、(x-1)2=m2+1 B、(x-1)2=m-1 C、(x-1)2=1-m D、(x-1)2=m+1

用直接开平方法解方程(x-3)2=8得方程的根为（ ）

（A）x=3+2 （B）x=3-2

（C）x1=3+2 ,x2=3-2 （D）x1=3+2,x2=3-2

一、填空题：（每空3分，共30分）

1、方程(x-1)(2x+1)=2化成一般形式是 ，它的二次项系数是 .

2、关于x的方程是(m2-1)x2+(m-1)x-2=0，那么当m 时，方程为一元二次方程；

当m 时，方程为一元一次方程.

3、若方程 有增根，则增根x=__________，m= .

4、(2003贵阳)已知方程 有两个相等的实数根，则锐角 =___________.

5、若方程kx2-6x+1=0有两个实数根，则k的取值范围是 .

6、设x1、x2是方程3x2+4x-5=0的两根，则 .x12+x22= .

7、关于x的方程2x2+(m2-9)x+m+1=0，当m= 时，两根互为倒数；

当m= 时，两根互为相反数.

8、若x1 = 是二次方程x2+ax+1=0的一个根，则a= ，

该方程的另一个根x2 = .

9、方程x2+2x+a-1=0有两个负根，则a的取值范围是 .

10、若p2-3p-5=0，q2－3q-5=0，且p≠q，则 .

二、选择题：（每小题3分，共15分）

1、方程 的根的情况是（ ）

（A）方程有两个不相等的实数根 （B）方程有两个相等的实数根

（C）方程没有实数根 （D）方程的根的情况与 的取值有关

2、已知方程 ，则下列说中，正确的是（ ）

（A）方程两根和是1 （B）方程两根积是2

（C）方程两根和是－1 （D）方程两根积是两根和的2倍

3、已知方程 的两个根都是整数，则 的值可以是（ ）

（A）-1 （B）1 （C）5 （D）以上三个中的任何一个

4、如果关于x的一元二次方程x2+px+q=0的两根分别为x1＝3、x2＝1，那么这个一元二次方程是（ ）

A. x2+3x+4=0 B. x2-4x+3=0 C. x2+4x-3=0 D. x2+3x-4=0

5、用配方法解下列方程时，配方有错误的是（ ）

A.x2-2x-99=0化为(x-1)2=100 B.x2+8x+9=0化为(x+4)2=25

C.2t2-7t-4=0化为 D.3y2-4y-2=0化为

三、解下列方程：(每小题5分，共30分)

（1） （2）

(3) (4)4x2-8x+1=0（用配方法）

(5) 3x2+5(2x+1)=0（用公式法） (6)

四、（本题6分）

(2003宁夏)某化肥厂去年四月份生产化肥500吨，因管理不善，五月份的产量减少了10％．从六月起强化管理，产量逐月上升，七月份产量达到648吨．那么，该厂六、七两月产量平均增长的百分率是多少？

五、（本题6分）

有一间长为20米，宽为15米的会议室，在它们中间铺一块地毯为，地毯的面积是会议室面积的一半，四周未铺地毯的留空宽度相同，则留空宽度为多少米？

六、（本题6分）

(2003南京)某灯具店购了一批某种型号的节能灯，共用去400元．在搬运过程中不慎打碎了5盏，该店把余下的灯每盏加价4元全部售出，然后用所得的钱又购了一批这种节能灯，且进价与上次相同，但购买的数量比上次多了9盏．求每盏灯的进价．

七、（本题12分，其中第(1)问7分，第(2)问是附加题5分）

(2003潍坊) 如图所示，△ABC中，AB=6厘米，BC=8厘米，∠B=90°，点P从点A开始沿AB边向B以1厘米/秒的速度移动，点Q从B点开始沿BC边向点C以2厘米/秒的速度移动.

(1) 如果P、Q分别从A、B同时出发，经过几秒，使△PBQ的面积等于8平方厘米？

(2) (附加题)如果P、Q分别从A、B出发，并且P到B后又继续在BC边上前进，经过几秒，使△PCQ的面积等于12.6平方厘米？

一、填空题：（每空3分，共30分）

1、方程(x–1)(2x+1)=2化成一般形式是 ，它的二次项系数是 .

2、关于x的方程是(m2–1)x2+(m–1)x–2=0，那么当m 时，方程为一元二次方程；

当m 时，方程为一元一次方程.

3、若方程 有增根，则增根x=__________，m= .

4、(2003贵阳)已知方程 有两个相等的实数根，则锐角 =___________.

5、若方程kx2–6x+1=0有两个实数根，则k的取值范围是 .

6、设x1、x2是方程3x2+4x–5=0的两根，则 .x12+x22= .

7、关于x的方程2x2+(m2–9)x+m+1=0，当m= 时，两根互为倒数；

当m= 时，两根互为相反数.

8、若x1 = 是二次方程x2+ax+1=0的一个根，则a= ，

该方程的另一个根x2 = .

9、方程x2+2x+a–1=0有两个负根，则a的取值范围是 .

10、若p2–3p–5=0，q2－3q–5=0，且p≠q，则 .

二、选择题：（每小题3分，共15分）

1、方程 的根的情况是（ ）

（A）方程有两个不相等的实数根 （B）方程有两个相等的实数根

（C）方程没有实数根 （D）方程的根的情况与 的取值有关

2、已知方程 ，则下列说中，正确的是（ ）

（A）方程两根和是1 （B）方程两根积是2

（C）方程两根和是－1 （D）方程两根积是两根和的2倍

3、已知方程 的两个根都是整数，则 的值可以是（ ）

（A）—1 （B）1 （C）5 （D）以上三个中的任何一个

4、如果关于x的一元二次方程x2+px+q=0的两根分别为x1＝3、x2＝1，那么这个一元二次方程是（ ）

A. x2+3x+4=0 B. x2-4x+3=0 C. x2+4x-3=0 D. x2+3x-4=0

5、用配方法解下列方程时，配方有错误的是（ ）

A.x2-2x-99=0化为(x-1)2=100 B.x2+8x+9=0化为(x+4)2=25

C.2t2-7t-4=0化为 D.3y2-4y-2=0化为

三、解下列方程：(每小题5分，共30分)

（1） （2）

(3) (4)4x2–8x+1=0（用配方法）

(5) 3x2+5(2x+1)=0（用公式法） (6)

四、（本题6分）

(2003宁夏)某化肥厂去年四月份生产化肥500吨，因管理不善，五月份的产量减少了10％．从六月起强化管理，产量逐月上升，七月份产量达到648吨．那么，该厂六、七两月产量平均增长的百分率是多少？

五、（本题6分）

有一间长为20米，宽为15米的会议室，在它们中间铺一块地毯为，地毯的面积是会议室面积的一半，四周未铺地毯的留空宽度相同，则留空宽度为多少米？

六、（本题6分）

(2003南京)某灯具店购了一批某种型号的节能灯，共用去400元．在搬运过程中不慎打碎了5盏，该店把余下的灯每盏加价4元全部售出，然后用所得的钱又购了一批这种节能灯，且进价与上次相同，但购买的数量比上次多了9盏．求每盏灯的进价．

七、（本题12分，其中第(1)问7分，第(2)问是附加题5分）

(2003潍坊) 如图所示，△ABC中，AB=6厘米，BC=8厘米，∠B=90°，点P从点A开始沿AB边向B以1厘米/秒的速度移动，点Q从B点开始沿BC边向点C以2厘米/秒的速度移动.

(1) 如果P、Q分别从A、B同时出发，经过几秒，使△PBQ的面积等于8平方厘米？

(2) (附加题)如果P、Q分别从A、B出发，并且P到B后又继续在BC边上前进，经过几秒，使△PCQ的面积等于12.6平方厘米？

01.已知三角形ABC的两边AB AC的长度是关于一元二次方程

x^2-(2k+2)x+k^2＝0的的两个根，第三边长为10，问K为何值时三角形ABC为等腰三角形？

02.证明关于x的方程（m^2-8m+17）x^2+2mx+1＝0 无论m为任何值，该方程都为一元二次方程

若a为有理数,试探求当b为何值时,关于x的一元二次方程x^2+3(a-1)x+(2a^2+a+b)=0的根为有理数?

2.设关于y的一元二次方程3(m-2)y^2-2(m+1)y-m=0有正整数根，试探求满足条件的整数m

1.已知a是关于x的一元二次方程x2-3x+m=0的一个根,-a是关于x的一元二次方程x2+3x-m=0.试求a的值.

2.如果我们知道方程(k2+2)x2+(5-k)x=1-3kx2 是关于x的一元二次方程.那么你能求得k的值吗?

3(x2+3x+4)(x2+3x+5)=6.通过仔细观察.巧妙解题(不准展开解题.)

4已知m.n是关于x的方程x2-(p-2)x+1=0的两个实数根,求代数式(m2+mp+1)(n2+np+1)的值

1.已知方程x+1/x=a+1/a的2根分别为a,1/a,则方程x+1/(x-1)=a+1/(a-1)的根是_______.

2.若a=3,b=2，则以a,b伟根的一元二次方程（二次项系数为一）是_________.

3.已知方程x^2-2x-1=0的2根是1+√2,1-√2,则分解因式:x^2-2x-1=________.

4.已知方程x^(K-2)+(k-2)x^2+x-k=0,当k取何值时，方程是一元二次方程？

1、 使实系数二次方程2mx[2]+(4m+1)x+2m=0有两个不相等的实数根的m的范围是（ ）

2、 满足方程x[2]+b[2]=(a-x)[2]的x的值是（ ）

3、 关于x的方程x[2]-(2a-1)x+a=5的一个解是1,则a的值为( )

4、 a,b,c为不全是0的3个实数,那么关于x的一元二次方程x[2]+(a+b+c)x+(a[2]+b[2]+c[2])=0的根的情况是（ ）

a 有2个负根 b 有两个正根 c 有2个异号实根 d 无实根

5、 满足x[2]+7x+c=0有实根的最大整数c是（ ）

6、 方程x[2]+1993x-1994=0和(1994x)[2]-1993·1995x-1=0的较小根依次为a，b，求ab的值

设关于x的一元二次方程x平方+px+q=0的两个根为A，B，且A，B满足lgA+lgB＝2，lg（A+B）＝2－2lg6+lg9,求一元二次方程及A，B的值！

1、已知a、b 为方程2x*x-5x+1=0的根，不解方程，求值：

（1）1/a+1/b (2)|a-b|

2、已知一元二次方程x*x-2mx-5+2m=0 的两根之差的绝对值等于4倍根号2，求m

方程 (m-3)x^(m^-7) +(m-2)+5=0

（1）m为何值时，方程是一元二次方程；

（2）m为何值时，方程是一元一次方程

X的2a+b次方-2×x的a-b次方+3=0是关于x的一元二次方程，求a、b的值。

已知a、b是一元二次方程x^2+2001x+1=0的两个根,则(1+2003a+a^2)(1+2003b+b^2)=( )

a、1 b、2

c、3 d、4

已知，a、b是一元二次方程x^2+px-1=0的两个实数跟，且3ab+b^2+2=8b。求p的值。

如果关于x的一元二次方程(ax+1)(x-a)=a-2的各项系数之和为3，求a的值，并解此方程

已知一元二次方程(ab-2b)x^2+2(b-a)x+2a-b=0有两个相等的实数根，求1/a+1/b

注：X＾2表示X的平方

回答者： 誓言今生 - 助理 二级 2-27 17:51

1.解下列关于x的方程：

(1)3a+4x=7x－5b; (2)xa－b=xb－a(a≠b)；

(3)m2(x－n)=n2(x－m)(m2≠n2);

(4)ab+xa=xb－ba(a≠b);

(5)a2x+2=a(x+2)(a≠0,a≠1).

2.填空：

(1)已知y=rx+b r≠0,则x=_______;

(2)已知F=ma,a≠0，则m=_________;

(3)已知ax+by=c，a≠0，则x=_______.

3.以下公式中的字母都不等于零.

(1)求出公式m=pn+2中的n;

(2)已知xa+1b=1m，求x；

(3)在公式S=a+b2h中，求a;

(4)在公式S=υot+12t2x中，求x.

答案：

1.(1)x=3a+5b 3； (2)x=ab; (3)x=mn m+n; (4)x=a2+b2 a－b (5)x=2a.

2.(1)x=y－b r； (2)m=Fa; (3)x=c－by a.

3.(1)n=p－2m m; (2)x=ab－am bm; (3)a=2s－bh h;

(4)x=2s－2υott2.

笔画2

汅 氾 氿 汀 汁 汃 汇 汉 汄 汈 氻

笔画3

汢 汑 汣 污 汌 汊 汋 丸 泛 汏 汐 汒 汓 汔 汕 汗 汘 污 汚 汛 汜 汝 江 池 汤 汲 汷

笔画4

沩 沨 洰 汼 汵 泤 沘 沪 沣 汯 沃 冱 汥 汦 汧 汨 汩 汪 汫 泐 泛 汭 汰 汱 汳 汴 汶 汸 汹 决 汻 汽 汾 沁 沂 沄 沅 沆 沇 沈 沉 沋 沌 沏 沐 沑 没 沔 沕 冲 沙 沚 沛 沜 沟 没 沤 沥 沦 沧 泲 沠 汮 汿 沎 沢 沞

笔画5

泦 泍 泘 泀 泋 沺 泻 泇 泎 泼 治 沼 沽 沾 沿 况 泂 泃 泄 泅 泆 泈 泊 泌 泏 泑 泒 泓 泔 法 泖 泗 泙 泜 溯 泞 泟 泠 泡 波 泣 泥 泧 注 泩 泪 泫 泬 泭 泮 泯 浅 泹 沫 沬 沭 沮 沰 沱 沲 河 沴 沵 沶 沷 沸 油 泱 泳 泷 泸 泺 泽 泾

笔画6

浕 浉 浄 浀 浂 洉 洡 洣 浐 洘 泚 浌 洼 洽 派 洿 浃 浇 浈 浊 测 浍 济 浏 浑 浒 浓 浔 泿 洱 涏 洀 洁 洂 洃 洄 洅 洆 洇 洈 洊 洋 洌 洎 洏 洐 洑 洒 洓 洔 洕 洗 洠 洙 洚 洛 洝 洞 涕 洢 洤 津 洦 洧 洨 泄 洪 洫 洬 洭 洮 洲 洳 洴 洵 汹 洷 洸 洹 洺 活 涎

笔画7

浗 淽 涥 浫 涃 浘 涩 洖 流 涧 浖 浙 浚 浛 浜 浝 浲 浞 浟 浠 浡 浢 浣 浤 浥 浦 浧 浩 浪 里 涚 浨 淓 涁 涟 洍 涍 浱 浵 浭 浮 浯 浰 浴 浶 海 浸 浃 浺 浻 浼 浽 浾 浿 涀 涂 涄 涅 涆 泾 消 涉 涊 涌 涐 涑 涒 涓 涔 涕 涖 涗 涘 涛 涝 涞 涠 涡 涣 涤 润 涨 浳 涜 涢 涋 涙

笔画8

渋 渒 渇 淗 済 淧 渵 渌 淕 淣 涭 淁 淂 淃 淄 淅 淆 淇 淈 淉 淊 淋 淌 淍 淎 淏 淐 淑 凄 淔 淖 淘 淙 泪 淛 淜 淝 淞 淟 淠 淡 淢 湕 渔 渂 涹 涪 涫 涬 涮 涯 涰 涱 液 涳 涴 淿 涵 涶 涷 涸 涺 涻 凉 涽 涾 涿 淀 淤 渌 淦 净 淩 * 淬 淮 淯 淰 深 淲 淳 淴 涞 混 渓 淸 淹 添 渀 渁 渃 渄 清 渊 渍 渎 渐 渑 渖 渗 渚 渠 涡 渮 渶 渏 湴 淭 渉 渆 渕

笔画9

渪 満 溂 湙 湾 渘 溉 湇 湼 渷 湐 湠 湚 湌 湅 湆 湉 湵 凑 湋 湍 湎 湏 湑 湒 湓 湔 湖 湗 湘 湛 湜 湝 浈 湟 湡 湢 闵 湦 涌 湨 湤 渼 滋 滑 滞 湽 渽 渊 渞 涣 湈 减 渜 渝 渟 渡 渢 渣 渤 渥 湥 湪 渧 渨 温 渫 测 渭 港 渰 渱 渲 渳 渴 游 渹 渺 渻 渿 湀 湁 湃 湄 湩 湫 湭 湮 湰 湱 湲 湳 湶 湷 湸 湹 湺 湻 湿 溃 溅 溚 溞 溠 溬 溲 溾 滁 溄 湂 溆 溋 溌 溇 溊 溁

笔画10

滟 滙 满 溤 溩 滪 澕 滛 滏 滘 滤 滣 溸 滜 溵 滝 滇 滈 滉 涤 滍 滐 滒 滓 滔 滖 滗 滢 滥 滦 滫 滭 溿 滨 滚 滠 溍 溎 溏 源 溑 溒 溓 溔 溕 准 溗 溘 溙 溛 滩 溜 溟 溡 溢 溣 溥 溦 溧 溨 溪 温 溭 溮 溯 溰 溱 溳 滊 溴 溶 溷 溹 溺 溻 湿 溽 滀 滂 滃 沧 滆 滶 漓 漠 漨 漭 漷 潃 滧

笔画11

潈 潌 溆 澚 漞 潉 潅 潊 滵 漝 漇 漈 滼 滮 滞 潒 潢 漜 潄 漌 漍 滰 滱 滳 滴 滹 滺 滻 滽 滚 满 漂 漃 漄 漅 漆 漉 漊 漋 漎 漏 漑 演 漕 漖 漗 漘 漙 漛 漟 漡 潳 漤 漥 漧 漩 漪 漫 渍 漮 漯 漰 漱 漳 漴 漶 漹 漺 漻 漼 漾 潀 潂 潆 潇 潋 潍 潎 潩 潴 澉 濄

笔画12

澘 澙 潱 潥 澓 澛 漽 潖 潐 澊 潓 潕 潗 潘 潜 潜 潝 潟 潠 潡 潣 潦 濆 濈 濍 濎 濐 漒 潶 潻 潏 潧 潨 潪 潫 潬 澅 潭 潮 浔 溃 潲 潵 滗 潸 潹 潺 潼 潽 潾 澁 澄 澄 澈 澋 澌 澍 澎 澏 澐 澑 澒 澔 澖 涧 澜 渑 澫 澳 澻 澾 澝

笔画13

濓 潚 潞 濇 濉 濗 濊 濋 濑 濒 濖 濏 澞 澟 澡 澢 澣 澥 澦 澧 澨 澪 澬 澭 澯 澰 澲 澴 澵 澶 澷 澸 澹 澺 澼 濨 澽 澿 激 濂 濅 蒙 濩 濭 瀄 濸

笔画14

湿 濵 濶 濔 涩 濣 濝 濚 濜 濞 濠 濡 濢 濥 濦 濧 濪 濮 濯 潍 濲 濴 濻 濿 漾 瀇 瀎 瀞 瀡 濹

笔画15

瀔 瀒 瀃 濽 瀀 瀂 滢 渎 瀈 瀊 瀌 瀍 瀐 瀑 瀓 瀢 潴

笔画16

瀭 濳 瀖 瀗 瀙 瀚 瀛 瀜 沥 潇 潆 瀣 瀤 瀥 濑 瀩 瀫 瀯 瀮 瀳 瀬

笔画17

瀿 灀 灁 灂 灆 灌 瀱 瀴 瀵 瀶 瀷 瀸 瀹 瀺 瀻 瀼 瀽

笔画18

灐 灅 灇 灈 灉 灊 灋 灍 灏

笔画19

灒 灔 灖 灗

笔画20

灜 灙 灚 灛 灡

笔画21

灞 灟 灠

笔画22

灢

笔画23

灎 灦

笔画24

灧 灨

笔画29

灪